15 Nov 2018 Martin Banov
IOTA: A Distributed Ledger of Everything for the Emerging Machine Economy
IOTA is neither blockchain-based nor driven by any of the commonly strapped consensus protocols that coordinate activity and designate roles within the network/system (such as Proof-of-Work, Proof-of-Stake, etc.)
IOTA instead employs a DAG (Directed Acyclic Graph) topology in how inter-dependencies and relationships between events occurring are structured in the distributed ledger, whose function is to guarantee the integrity of the data flowing within the system. DAGs generally allow for much more flexibility and a range of possible implementations (of algorithms, programs, strategies, etc.) in a wide variety of conceivable applications and scenarios.
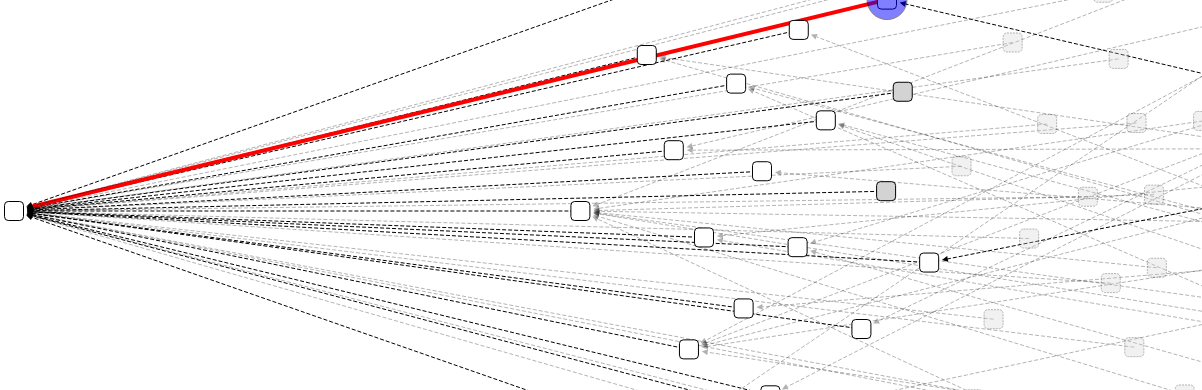
DAG: chains of transactions without blocks.
IOTA is particularly geared towards the future landscape of the Internet-of-Things and the explosion of constantly absorbed data accompanying those networks of connected devices (e.g., sensors and actuators) on a global scale. As such, IOTA focuses on the emerging machine-to-machine economies and their associated markets (e.g., data-driven insights marketplace, machine learning, and AI, outsourced computations and fog computing, etc.) - "data is the new crude", as is often said these days.
The DIKW Pyramid/Hierarchy is used to represent the structural-functional relationships between data, information, knowledge, and wisdom. "Typically information is defined in terms of data, knowledge in terms of information, and wisdom in terms of knowledge" (Rowley, 2007).
One of IOTA's core founders, Belarus-based Sergei Ivancheglo (better known as Come-from-Beyond), is well-known in the "crypto" community since the early days of bitcointalk.org and as the creator of the NXT platform, which marked the first successful implementation of a Proof-of-Stake consensus.
Other founding members include Mathematics Professor Serguei Popov and Norwegian David Sønstebø. As an entity, IOTA itself is based/registered as a non-profit foundation in Berlin, Germany and dedicated to developing industry standards and open-source protocols for the IoT - a largely uncharted territory, but one of critical importance in the future world on the horizon (just like quantum-proof cryptography) that will inevitably determine and shape the dynamics of interaction and nature of governance in many domains, both institutional and socio-technical/socio-economic.
Ternary
IOTA combines a number of exotic technologies in what is often seen as an unconventional and unorthodox approach to distributed systems design and engineering - its choice of ternary-based logic circuitry baffles many. Since hardware/processors in use today employ binary (zeroes and ones), while balanced ternary (-1, 0, 1) is mostly limited to specialized custom hardware in research labs, IOTA's hardware component - the trinary JINN microprocessor, intended to support large-scale distributed computing, is integral to the project's vision and has been quietly in the making since 2014 (IOTA's reference implementation presently emulating ternary logic on binary circuitry).
It has been noted that ternary logic gates more closely/accurately mirror/reflect how actual neurons in a nervous system process data, its capacity to contain more in less relevant to systems economies and self-sustainable/self-organizing complex assemblies (among the components necessary for enabling entire cities to operate within a technological mesh).
The Tangle
IOTA's idiosyncratic ledger-of-everything is a DAG-valued stochastic process called the tangle. The tangle is a complex mathematical object with a random structure defined by a distinct random agent, a random walk. Unlike the deterministic world of walled-off blockchain systems, the tangle is designed to deal with probabilities (i.e., is Bayesian in nature). Instead of miners validating and serially appending transactions on a single lane (i.e., the canonical ledger) and pocketing fees in return, in IOTA every transaction must reference two previous transactions in a pay-it-forward manner which allows for fast, feeless transactions and thus, minimal friction (an important property for attaining perfect information in a complete market).

IOTA tangle visualized. Source: tangle.glumb.de
The tangle is essentially IOTA's data transport/communication layer between devices and the backbone foundation for more sophisticated compositions and layers of functionality.
A visual simulation of the tangle, with adjustable parameters, can be found here.
A tangle visualizer (of main, test, and spam nets) can be found here.
Qubic
Qubic is the IOTA solution to oracles (data providers external to the system), "smart contracts" (called qubits here), and outsourced/distributed computations. As a matter of fact, IOTA is really the foundation/stepping stone for the more ambitious Qubic project. The general underlying concept of Qubic is that of quorum-based computations.
A quorum is the minimum number of votes that a distributed transaction has to obtain in order to be allowed to perform an operation in a distributed system. A quorum-based technique is implemented to enforce consistent operation in a distributed system.
Source: Wikipedia.
Outsourcing heavier computational tasks to more capable devices available within reach and willing to process the tasks/qubits (for a set price) is particularly important for the IoT, which is often comprised of devices with limited available computational resources.
The programming language used to define "smart contract" qubits is called Abra (under active development). It is a functional style language supporting IOTA's trit vector data type. It has no control structures (no if-then-else, no for or while loops) or built-in operators (e.g., multiplication, division, subtraction, etc.), only function expressions within five basic operations (such as function call, a lookup table which allows every operation to be expressed as a lookup, etc.)
The Abra railroad syntax diagram can be found here.

Tip Selection Algorithms and Markov Chain Monte Carlo
Unapproved transactions are referred to as tips and the method for nodes to choose tips to approve is called the tip selection algorithm (nodes are not obliged to follow the recommended algorithm, however, if most do follow it, the rest have an incentive to likewise do so). Tip selection is performed via a weighted random walk from genesis to tip (biased towards transactions with more cumulative weight, or more transactions referencing them, which introduces an incentive to approve new, incoming transactions). As the walk is performed twice, two tips are chosen - designated as trunkTransaction and branchTransaction.
Validation takes place more or less in the following fashion: using the Random Walk Monte Carlo method (RWMC), select 100 new transactions (tips) and calculates how many tips directly or indirectly will reach the transaction. If it's below 50%, the transaction is not yet validated. If it's above 50%, the transaction has a fair chance of being validated. If it's 99%, the transaction is considered validated/confirmed.
In statistics, Markov chain Monte Carlo (MCMC) methods comprise a class of algorithms for sampling from a probability distribution. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain a sample of the desired distribution by observing the chain after a number of steps. The more steps there are, the more closely the distribution of the sample matches the actual desired distribution.
Markov chain Monte Carlo methods are primarily used for calculating numerical approximations of multi-dimensional integrals, for example in Bayesian statistics, computational physics, computational biology, and computational linguistics.
In Bayesian statistics, the recent development of Markov chain Monte Carlo methods has been a key step in making it possible to compute large hierarchical models that require integrations over hundreds or even thousands of unknown parameters.
In rare event sampling, they are also used for generating samples that gradually populate the rare failure region.
Source: Wikipedia
The introduction of Markov Chain Monte Carlo (MCMC) algorithms is one essential contribution of IOTA to the domain of "crypto-currencies" and distributed systems economies. These algorithms pick the attachment sites on the tangle for arriving transactions and gradually optimize and sort out the arsenal of possible solutions and available paths in different emerging circumstances and regimes of activity.
For a more detailed descriptions, see "Anatomy of a transaction" from the official documentation.
Coordinator (COO)
To bootstrap the network in its infancy stages until it acquires enough critical mass (throughput and confirmation times in the IOTA tangle are a function of the network's size) and in order to during that phase ensure protection against certain attack vectors, IOTA relies on a set of nodes run by the IOTA foundation known as the coordinator. The coordinator checkpoints valid transactions by issuing periodic zero-value milestone transactions (at the pace of one per minute on mainnet) used to reference valid transactions.
As the network evolves and the pace of activity/network effects pick up, the training wheels of the Coordinator will be gradually distributed/decentralized and eventually completely done away with when the necessary conditions to safely do so emerge.
Economic Clustering
Ivancheglo published a blog post on Economic Clustering earlier in June, describing it so:
So how IOTA may look in a few years when EC is deployed to the mainnet? I envision the following picture.
There is Cluster 0. It consists of nodes interacting via the Internet, main economic cluster actors - big companies - run special software playing the role of a distributed Coordinator. This software does only one thing — it signals that a particular actor has seen certain transactions and will accept them as legitimate ones with some probability. There are thousands of other clusters formed by nodes interacting via the Internet of Things. Some of them are connected to Cluster 0 directly. A single cluster can be a group of devices in a building, in a park, in a town, or even on a stretch of road. The structure depends on economic activity in an area. A single cluster is connected to several other clusters, mainly adjacent ones (in spatial meaning). Each cluster processes its own transactions and transactions of the neighbor clusters, all the other transactions are ignored because they simply don’t reach the cluster.
The notion of Economic Clustering has important implications for scalability in general, specialization, and economic diversification within a system. Ethereum's Plasma side-chains can also be seen as a form of Economic Clustering (i.e., certain economic activities localized on their appropriately optimized side-chain branches).

Local Modifiers
Among amendments and improvements to the mathematical models, it is interesting to mention local modifiers, as described by Popov in a paper published earlier in 2018 (“Local Modifiers in the Tangle”) - it suggests that nodes can interact in different ways with the ledger, depending on various local factors and information available to them (as opposed to all network participants interpreting the same ledger in the same way, which inevitably leads to bottlenecks). This local view of the node is somewhat reminiscent of Holochain's agent-centric ontology and the notion of holographic consensus (as implemented by DAOstack), intertwining different angles/perceptions of the same in a more holistic view.
Nash Equilibrium
Decision making is an aspect implicit in every dynamic system of interactive relations and Nash equilibrium is an important concept in IOTA's theoretical model. A Nash equilibrium is a game theory concept characterizing a state in which every actor has optimized his strategy in alignment with all the other participants' choices - simply put, it refers to laws that don't require policing or enforcement even in the absence of enforceable mechanisms (a trivial example being traffic light signals - it makes sense that everybody would follow then since nobody will gain any advantage by not doing so).
A paper authored by Popov and others entitled "Equilibria in the Tangle" from March 2018, proves the existence of a Nash equilibrium on the tangle in produced simulations where it is demonstrated that even though there are no strict (but only approximate) rules for choosing transactions when a large number of nodes follow some reference rule, it is to the benefit of any such node to stick to a rule of the same kind ("selfish" participants will cooperate with their tangle as there is no incentive to deviate).
This makes sense in the context of IOTA and the overall logic of the system where users are seen as the devices they interface with and as such a byproduct of the network itself. These premises create an environment that is collaborative in nature, as users contribute to the stability and security of the network simply by using it.
In a later blog post, Popov explains:
In a non-cooperative game between two or more players, a Nash Equilibrium is achieved when — given the strategies of the other players — each of the players has nothing to gain by deviating from his own current strategy. In certain cases, such a Nash Equilibrium can occur where some or all the players are left worse off in comparison to the outcome of a cooperative game, such as the well-known Prisoner’s Dilemma game. In other cases, a Nash Equilibrium can occur in a Pareto-optimal outcome where no other possible outcome would make any player better off without making at least one player worse off. Because IOTA is a decentralized, distributed, and permissionless network of nodes, it must be assumed that some proportion of the nodes in this system will be playing a non-cooperative game, choosing only to maximize their own self-interest. It is therefore important to understand where an equilibrium might occur in this particular game given the presence of selfish (or “greedy”) nodes. Would it devolve into a tragedy of the commons? Or would the Nash Equilibrium occur at a Pareto-efficient outcome? Would a Nash Equilibrium exist at all in this situation?
ISOs
Recently, IOTA introduced an alternative (to the ICO), a more sustainable model for funding - an ISO, or Initial Service Offering. While ICOs center around tokens as gambling chips (consequently opening the floodgates of scams, get-rich-quick schemes, and speculative frenzies) and future promises (often in the format of clumsily stitched together with white papers) where they might possibly turn into a kind of company scrip should they succeed, the ISO model focuses instead on a public service provided, encouraging people to invest in projects and initiatives they are actually/genuinely interested in, facilitating sustainable and smooth development over a period of time with an engaged, active community.
The ISO model uses the IOTA native token as a base currency and grants ISO investors to receive free services (or compensation of IOTA tokens, should the project fail). It is much less speculative in nature, building trust and alleviating much of the regulatory burdens surrounding ICOs and "cryptocurrencies" in general. It is a model that reduces associated risks and focuses on supporting useful services and their development and integration into the IOTA ecosystem.
Links and Resources
White paper by Serguei Popov.
GitHub (reference implementation and libraries).
Documentation, FAQ and academic papers.
IOTA IOTA explained Distributed Ledger IOTA analysis Directed Acyclic Graph DAG Internet of things IoT Sergey Ivancheglo Serguei Popov David Sønstebø IOTA Ternary IOTA tangle IOTA qubic IOTA guide IOTA coordinator IOTA development Economic Clustering Masked Authenticated Messaging (MAM)






























